Topologieoptimierung eines Balkens
Die Topologieoptimierung unterstützt im Allgemeinen den Konstrukteur bei dem Entwurf einer (Neu-)Konstruktion, indem optimale Kraftpfade innerhalb des zur Verfügung stehenden Bauraums bestimmt werden. Darauf basierend wird das Material im Bauraum verteilt, sodass eine günstige Grundgestalt (Topologie) des Bauteils für die vorgegebene Belastungssituation entsteht. Neben dieser klassischen Steifigkeitsoptimierung können grundsätzlich auch weitere Bauteileigenschaften - wie zum Beispiel Spannungen - minimiert bzw. maximiert werden.
Dieser Optimierungsprozess benötigt in der Praxis jedoch häufig die Unterstützung von Simulationsexperten, da die iterative Anpassung der Bauteilgestalt zumeist auf den Ergebnissen mehrerer Finite-Elemente-Analysen basiert. Um auch ohne vertiefte Simulationskenntnisse einen ersten Einblick in die Topologieoptimierung zu bekommen, erlaubt dieser Online-Optimierer verschiedene Modell- und Optimierungsparameter zu variieren und deren Einfluss auf den Designvorschlag zu beobachten.
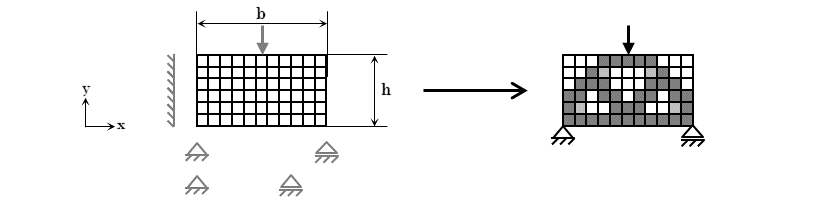
Der Bauraum des Optimierungsmodells ist hier ein Balken, der beispielsweise als Kragbalken (Feste Einspannung) oder als Messerschmitt-Bölkow-Blohm-Balken (Fest-Los-Lagerung) berechnet werden kann. Daneben kann der Ort und die Richtung der wirkenden Einzellast vom Nutzer vorgegeben werden, um verschiedene Belastungssitationen zu untersuchen. Damit der Optimierungsalgorithmus - hier das Optimalitätskriterienverfahren - nicht den gesamten Bauraum und damit eine Triviallösung als Design vorschlägt, ist der Füllgrad vorzugeben. Dieser beschreibt das Verhältnis zwischen dem Ziel- und dem Ausgangsvolumen.
Hinweis: Der Optimierungsparameter p des SIMP-Ansatzes (Solid Isotropic Material with Penalization) erlaubt für fortgeschrittene Untersuchungen die Steuerung des Optimierungsalgorithmus. Im Allgemeinen wird ein Wert von 2,6 bis 4 empfohlen - weiterführende Informationen finden sich in der unten stehenden Literatur.
- Rieg, Frank; Hackenschmidt, Reinhard; Alber-Laukant, Bettina: Finite Elemente Analyse für Ingenieure (Grundlagen und praktische Anwendungen mit Z88Aurora). 6. München: Carl Hanser Verlag, 2019
- Olhoff, Niels; Bendsoe, Martin P.; Rasmussen, John: On CAD-integrated structural topology and design optimization. Computer Methods in Applied Mechanics and Engineering 89 (1991), Nr. 1-3, S.259-279
- Billenstein, Daniel: Finite-Elemente-Strategien zur Berücksichtigung des elastischen Umfeldes in der Topologieoptimierung. Universität Bayreuth, Dissertation: 2019
- Frisch, Michael: Entwicklung eines Hybridalgorithmus zur steifigkeits- und spannungsoptimierten Auslegung von Konstruktionselementen. Universität Bayreuth, Dissertation: 2015