Bi­lin­eare Inter­po­lation auf be­lie­bigem Vier­eck

Die bilineare Interpolation wird gerade in der Bildbearbeitung zumeist auf rechtwinklige Gitter angewendet. Liegt jedoch ein beliebiges unstrukturiertes Gitter vor - wie beispielsweise häufig bei der Finite-Elemente-Analyse - muss das Gitter zunächst auf ein Rechtwinkliges transformiert werden. Hierzu wird das Viereck des Ausgangsgitters auf ein Einheitsquadrat im lokalen r-s-Koordinatensystem transformiert und die lokalen Koordinaten des Interpolationspunktes ermittelt. Nach dieser Transformation liegt wieder ein Standard-Interpolationsproblem vor, das mit den bekannten bilinearen Interpolationsgleichungen gelöst werden kann.

Die beschriebene Problemstellung tritt sehr häufig im Bereich der Finite-Elemente-Analyse auf: Beispielsweise liegen nach erfolgreichem Rechenlauf die Verschiebungsergebnisse nur an den Eckknoten des Elementes vor - ist jedoch der Ergebniswert an einer Stelle innerhalb des Elementes von Interesse, kann dieser etwa mit der bilinearen Interpolation berechnet werden. Ein solches ebenes Viereckelement ist nachfolgend mit einem exemplarischen Abfragepunkt X (Index: ?) dargestellt:

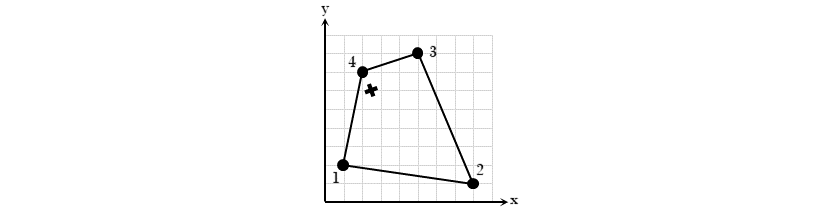
Beachte: Die Eckpunkte des Vierecks müssen gegen den Uhrzeigersinn definiert werden - dahingegen können die Funktionswerte der Eckpunkte auch weggelassen bzw. zu Null gesetzt werden, sofern nur die lokalen Koordinaten gewünscht sind.